Warning: full frontal mathematics. (If you've had a couple of semesters of calculus, you should be good.)
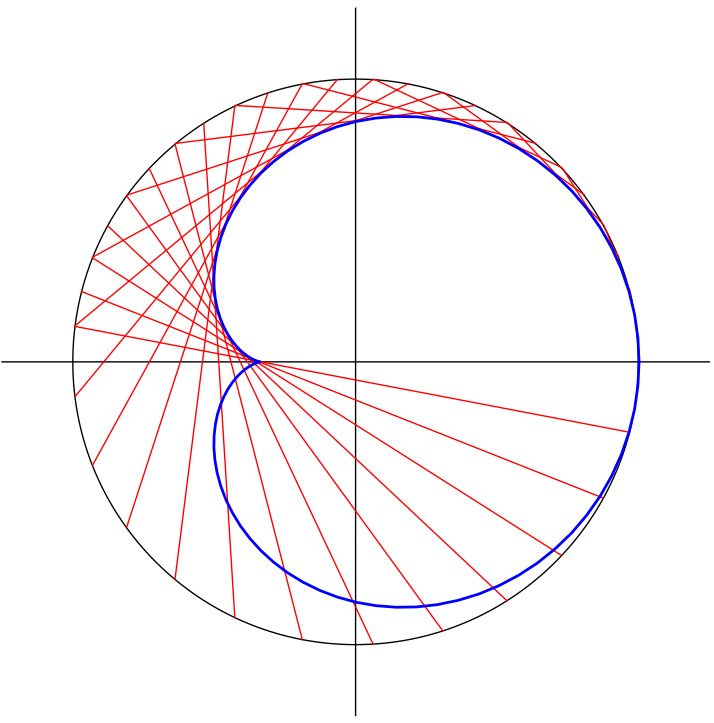
This shows a cardioid as the envelope of chords in the unit circle. Each chord connects the point on the circle at an angle \(\theta\) to the point at angle \(2\theta\), with \(0\le\theta\lt\pi\). That is, the chord connects \((\cos\theta,\sin\theta)\) to \((\cos2\theta,\sin2\theta)\). Here, there are 25 chords drawn, for \(\theta = k\pi/25\) where \(0\le k\le25\).

The cardioid is given by the following parametric curve: \[ {\renewcommand{\arraystretch}{1.5} \begin{array}{l}x=\tfrac23(1+\cos t)\cos t - \tfrac13 \\ y=\tfrac23(1+\cos t)\sin t\end{array}} \] What's interesting is that the cusp is not at the origin; it's at \(x=-\tfrac13\). The cardioid extends from \(x=-\tfrac12\) to \(x=1\). But this is a cardioid: it's the polar curve \(r=1+\cos\theta\) converted to parametric form using \(x=r\cos\theta\) and \(y=r\sin\theta\), then scaled and translated.
I saw this on Twitter (via @stevenstrogatz on Twitter), on a page by David Richeson, I Heart Cardioids (accessed April 2018). They gave a slightly different set-up of the following; they looked at \(r=2(1+\cos\theta)\) inside the circle of radius \(3\) with center \((1,0)\). But my goal here was to verify this for myself.
I should mention that I didn't notice they used an off-center circle; I started out with the circle of radius \(2\) centered at the origin, with the cardioid \(r=1+\cos\theta\). It took me quite a while to realize this isn't correct!
It's possible to find the envelope curve directly. One strategy is to find the intersection point of two chords that are close to each other. So you would look at two chords as described above, with angle \(\theta\) and with angle \(\theta+d\theta\), and then let \(d\theta\to0\). This turns out to be hard work. But if you already know the envelope curve (as given above), it is fairly easy to verify.
To verify the curve given above is the envelope curve, first use double-angle identities to write the parametric equations as: \[ {\renewcommand{\arraystretch}{1.5} \begin{array}{l}x=\tfrac13\cos 2t + \tfrac23\cos t \\ y=\tfrac13\sin 2t + \tfrac23\sin t \end{array}} \] All we need to do is verify that the line from \((\cos t,\sin t)\) to \((\cos 2t,\sin 2t)\) is tangent to this curve.
We do this as follows: Verify that the point \[(x,y)=\big(\tfrac13\cos 2t + \tfrac23\cos t , \tfrac13\sin 2t + \tfrac23\sin t\big)\] is on the line \(y-y_0=m(x-x_0)\), where \((x_0,y_0)=(\cos t,\sin t)\) and \[ m = \frac{\sin 2t - \sin t}{\cos 2t-\cos t}. \] That is, verify the point satisfies \[ y-\sin t = \left(\frac{\sin 2t - \sin t}{\cos 2t-\cos t}\right)(x-\cos t) \] If we substitute the values of \(x\) and \(y\), this becomes \[ \tfrac13\sin 2t + \tfrac23\sin t - \sin t = \left(\frac{\sin 2t - \sin t}{\cos 2t-\cos t}\right)\big(\tfrac13\cos 2t + \tfrac23\cos t-\cos t\big) \] or \[ \tfrac13\sin 2t - \tfrac13\sin t = \left(\frac{\sin 2t - \sin t}{\cos 2t-\cos t}\right)\big(\tfrac13\cos 2t - \tfrac13\cos t\big) \] or \[ \sin 2t - \sin t = \left(\frac{\sin 2t - \sin t}{\cos 2t-\cos t}\right)\big(\cos 2t - \cos t\big) \] and now it becomes clear.
Then all that is needed is to verify that the slope of this line matches the slope of the cardioid at the point. The slope of the cardioid is \[ m = \frac{dy/dt}{dx/dt}= \frac{\tfrac23\cos2t+\tfrac23\cos t}{-\tfrac23\sin2t-\frac23\sin t} = - \frac{\cos 2t+\cos t}{\sin 2t+\sin t}. \] The claim is that this matches \[ m = \frac{\sin 2t - \sin t}{\cos 2t-\cos t}. \] But this follows from the identity \[ \frac{\cos\alpha-\cos\beta}{\sin\alpha-\sin\beta} = - \frac{\sin\alpha+\sin\beta}{\cos\alpha+\cos\beta} \] This is easy to verify: Write \[ \cos^2\alpha+\sin^2\alpha = \cos^2\beta+\sin^2\beta \] as \[ \cos^2\alpha - \cos^2\beta = \sin^2\beta-\sin^2\alpha \] or \[ (\cos\alpha-\cos\beta)(\cos\alpha+\cos\beta) = (\sin\beta-\sin\alpha)(\sin\beta+\sin\alpha) \] and just divide.